Red-Black Tree : 기존 이진 탐색 트리에서 탐색, 삽입, 삭제의 시간 복잡도는 O(h)이다. 즉 , 트리의 높이에 비례한 만큼의 시간이 걸린다. 원소들이 트리에 잘 분산 되어 있다면 별 문제가 없지만, 한 쪽으로 치우친 트리 (skewed tree)의 경우에는 높이가 n이 되어 시간 복잡도가 O(n)이 된다.
이러한 이진 탐색 트리에 색(Red, Black)이라는 속성을 추가하여 최악의 상황이라도 시간 복잡도 O(log n)을 유지한다.
- 조건
1. 모든 node는 Red 혹은 Black의 색을 갖는다.
2. root node는 항상 Black이다.
3. NIL node(= leaf node)는 Black이다.
4. Red node의 자식 node는 항상 Black node이다. (= Red node는 연달아 나타날 수 없으며, Black node만 Red node의 부모 node가 될 수 있다.)
5. 어떤 node에서 leaf node까지 도달하는 과정에서 거쳐간 Black node의 수의 합은 항상 같다.
이 원칙을 지키기 위해 회전(rotation)을 해야 함.
- 최악의 경우에도 시간 복잡도를 O(log n)을 유지 할 수 있는 이유
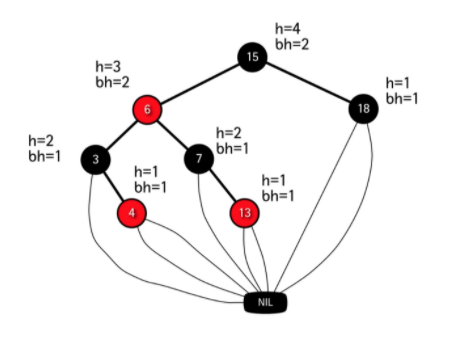
v : 해당 node
h(v) : node의 높이 (v로 부터 leaf node까지의 가장 긴 경로의 수)
bh(v) : 해당 node에서 leaf node까지의 black node의 개수 (v 본인 제외)
1. Red-Black Tree의 내부 node 개수 (n) : Root가 v인 node의 sub tree는 적어도 (2^bh(v)) - 1 개의 내부 node를 가짐을 증명해야 함.
h(v)에 대한 수학적 귀납법으로 증명할 수 있다. h(v) = 0 이면 v는 NIL node이므로 이 node를 root로 하는 sub tree는 (2^0) - 1 = 0개의 내부 node를 가진다.
이번엔 아래 그림처럼 v가 양의 높이를 가지고 두 자식을 가지는 내부 node라 하자
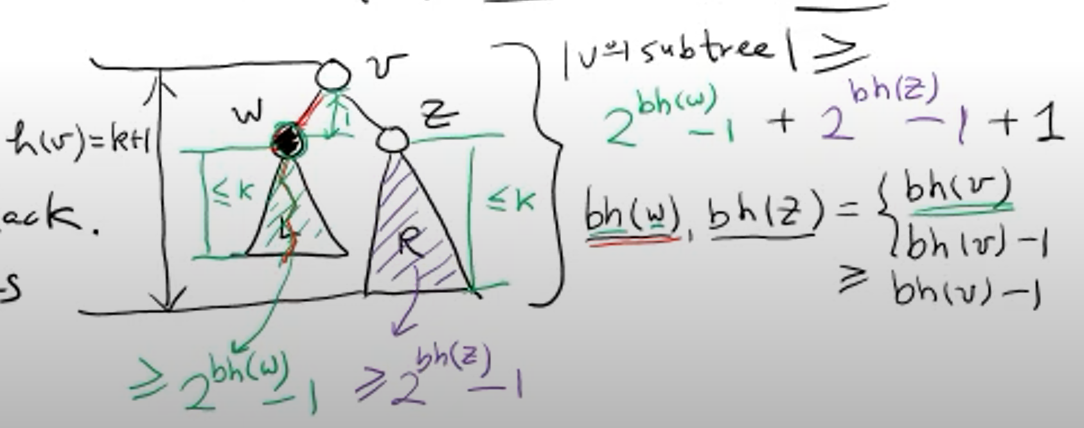
각 자식은 자신의 색이 Red or Black에 따라 bh(v) - 1 또는 bh(v)의 높이를 가진다. 적어도 몇 개의 내부 node를 가지는 가를 알아보는 상황이기 때문에 둘다 bh(v) - 1라고 해도 문제가 없다. 따라서 v를 root로 하는 sub tree는 적어도
(2^(bh(v) - 1)) - 1 + (2^(bh(v) - 1)) - 1 + 1 (v 자기 자신) = (2^bh(v)) - 1개의 내부 노드(n)를 가진다.
2. 조건 4에 의해 root에서 leaf로 가는 단순 경로의 node 중 절반 이상이 Black이다.
즉, root의 bh(v)는 적어도 h / 2이다.
1과 2의 결과를 조합하면 n >= (2^bh(v)) - 1 >= (2^(h / 2)) - 1이므로 이항하여
n + 1 >= 2^(h / 2)로 바꾸고, 양변에 log를 씌우면 log(n + 1) >= h / 2 -> h <= 2log(n + 1) 이 된다.
h <= 2log(n + 1) 이라는 사실에 의해 탐색, 삽입, 삭제와 같은 연산은 Red-Black Tree를 이용하면 최악의 상황에서도 시간복잡도 O(log n)가 됨을 알 수 있다.
'개발에 도움이 되는 > 자료구조 & 알고리즘' 카테고리의 다른 글
| 트리(Tree) (0) | 2022.01.01 |
|---|---|
| 그래프(Graph) (0) | 2022.01.01 |
| 해시 테이블(Hash Table) (0) | 2022.01.01 |
| 스택(Stack), 큐(Queue) (0) | 2022.01.01 |
| 배열(Array), 연결 리스트(Linked List) (0) | 2022.01.01 |



