- 이진 탐색 트리 (Binary Search Tree)
정렬된 이진 트리로 다음과 같은 규칙을 갖는다.
1. 이진 탐색 트리의 노드에 저장된 값은 유일하다.
2. 부모의 값은 왼쪽 하위 트리 노드들의 값보다 항상 크다.
3. 부모의 값은 오른쪽 하위 트리 노드들의 값보다 항상 작다.
4. 왼쪽 및 오른쪽 하위 트리도 각각 이진 검색 트리여야 한다.

BST의 검색에 대한 시간 복잡도는 균형 상태면 O(log n)의 시간이 걸리고 불균형 상태(편향 트리 Skewed Tree)라면 최대 O(n)의 시간이 걸린다. 이러한 문제를 막기 위해 Rebalancing 기법이 등장하였다. (ex. Red-Black Tree 등)

- 이진 탐색 트리의 연산
1. 검색 : 이진 탐색 트리에서 특정 요소의 위치를 찾는다.
1) 루트에서 시작
2) 검색 값을 루트와 비교 -> 루트보다 작으면 왼쪽에 대해 재귀하고 크다면 오른쪽으로 재귀
3) 일치하는 값을 찾을 때까지 절차 반복
4) 검색 값이 없으면 null 반환

2. 삽입 : 데이터를 삽입하는 작업(중복은 허용하지 않음), 새로운 값은 항상 리프 노드에 삽입
1) 루트에서 시작
2) 삽입 값을 루트와 비교 -> 루트보다 작으면 왼쪽으로 재귀하고 크다면 오른쪽으로 재귀
3) 리프 노드에 도달한 후 노드보다 크다면 오른쪽 작다면 왼쪽에 삽입

3. 삭제 : 특정 노드를 삭제, 삭제하는 상황은 3가지가 있다.
- 삭제할 노드가 리프 노드인 경우 : 노드를 삭제하기만 하면 된다.

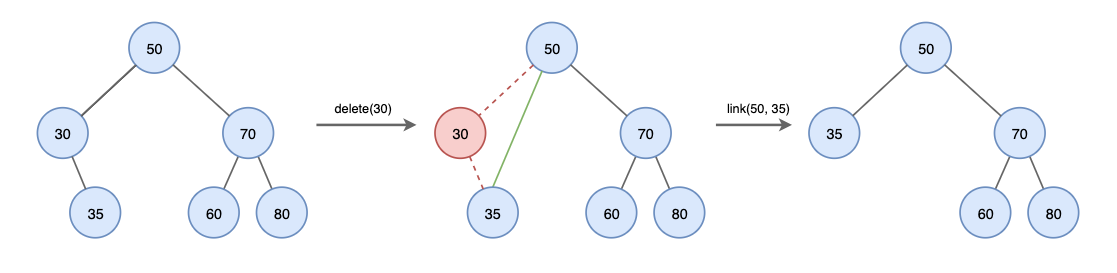
- 삭제할 노드에 자식이 하나만 있는 경우 : 노드를 삭제하고 자식 노드를 삭제된 노드의 부모에 직접 연결한다.
- 삭제할 노드에 자식이 둘 있는 경우 : successor 노드를 찾는 과정 추가
- successor node : 오른쪽 서브트리의 최솟값
1) 삭제할 노드를 찾음
2) 삭제할 노드의 successor 노드를 찾음
3) 삭제할 노드와 successor 노드의 값을 바꿈
4) successor 노드를 삭제

'개발에 도움이 되는 > 자료구조 & 알고리즘' 카테고리의 다른 글
| Float(부동 소수점 자료형)의 숫자 표현법 (0) | 2022.01.08 |
|---|---|
| 힙(Heap) (0) | 2022.01.02 |
| 이진 트리(Binary Tree) (0) | 2022.01.02 |
| 트리(Tree) (0) | 2022.01.01 |
| 그래프(Graph) (0) | 2022.01.01 |



