- 힙 (Heap)
이진 힙(binary Heap)이라고도 하며, 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전 이진트리(Complete Binary Tree)를 기본으로 한 자료 구조
오로지 부모 노드의 값과 자식 노드의 값 사이에는 대소관계가 성립한다. 형제 사이에는 대소관계는 의미 없음.
우선 순위 큐, 다익스트라 알고리즘 등에 사용
- 힙의 종류
1. 최대 힙 (Max Heap) : 부모 노드의 값이 자식 노드의 값보다 크거나 같은 힙, 가장 큰 값이 루트 노드에 있음

2. 최소 힙 (Min Heap) : 부모 노드의 값이 자식 노드의 값보다 작거나 같은 힙, 가장 작은 값이 루트 노드에 있음

- 힙 표현 : 일반적으로 배열로 표현, 개발 편의성과 가독성 때문에 배열 인덱스 1부터 사용
1) 노드 i의 부모노드 인덱스 : i / 2
2) 노드 i의 왼쪽 자식 노드 인덱스 : 2 * i
3) 노드 i의 오른쪽 자식 노드 인덱스 : 2 * i + 1

- 힙 연산 (최대 힙을 기준으로)
1. Heapify : 힙 속성을 유지하는 작업, 위에서 아래로 내려가면서 작업
1) 요소 값과 자식 노드 값을 비교
2) 만약 자식 노드 값이 크다면 왼쪽과 오른쪽 자식 중 가장 큰 값으로 교환
3) 힙 속성이 유지 될 때까지 1, 2번 과정을 반복

2. Build Heap : 완전 이진 트리를 Heap 구조로 만드는 작업
1) 리프 노드를 제외한 나머지 노드 중 마지막 노드부터 루트 노드까지 차례로 max_heapify를 수행
3. Peek : Heap의 최대 요소를 반환하는 작업 , Max Heap에서 최댓값은 항상 루트에 있으므로 루트 값을 반환
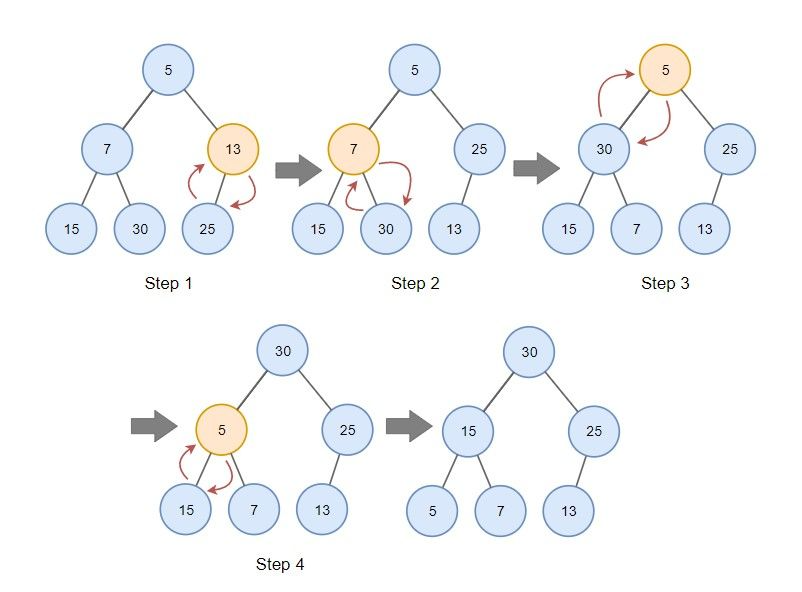
4. Extract : Heap의 최대 요소를 추출하는 작업, 추출 후 Heap 마지막 요소를 루트 노드에 배치 그 다음에 max_heapify 수행

5. Increase Value : Max Heap에서 사용하는 작업 (Min Heap에서는 Decrease Value 사용), 값을 증가 시킨 후 부모 노드와 비교하여 Heap 속성에 위배하는 경우 부모 노드와 값을 바꿈

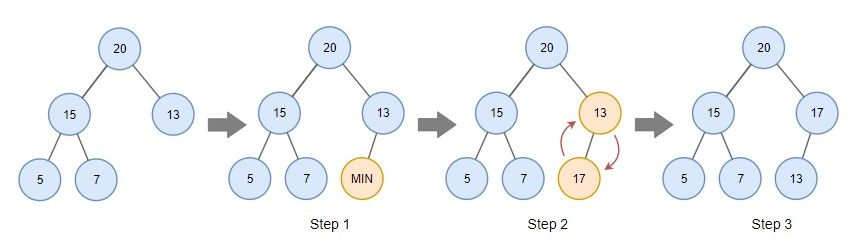
6. Insert : Heap의 끝에 최솟값을 삽입 후 Increase Value 함수를 호출하여 추가된 값을 삽입할 값으로 증가시키고 Heap 속성을 유지
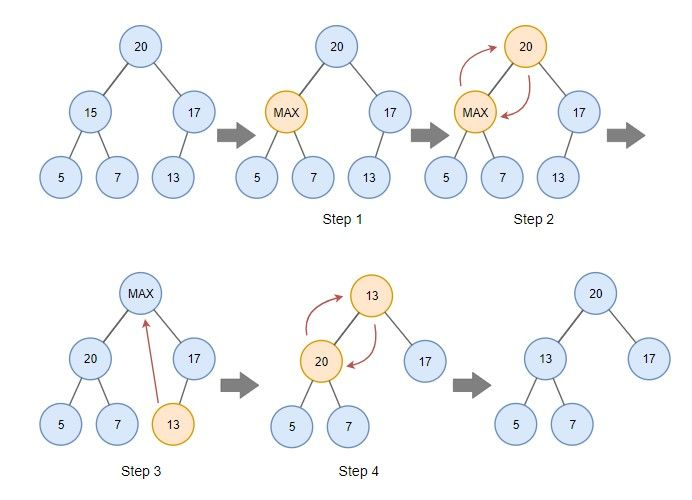
7. Delete : Increase Value를 수행하여 삭제할 요소를 Max값으로 증가시키고 루트 노드에 위치시킨 뒤, Extract를 수행하여 루트 노드 값을 추출
'개발에 도움이 되는 > 자료구조 & 알고리즘' 카테고리의 다른 글
| 정렬(Sort) 알고리즘 (0) | 2022.01.14 |
|---|---|
| Float(부동 소수점 자료형)의 숫자 표현법 (0) | 2022.01.08 |
| 이진 탐색 트리(Binary Search Tree, BST) (0) | 2022.01.02 |
| 이진 트리(Binary Tree) (0) | 2022.01.02 |
| 트리(Tree) (0) | 2022.01.01 |



